2. Discontinuidades
Importante
Una discontinuidad se dice evitable en \(x= a\) si existe el límite de la función en el punto y es finito, pero no coincide con el valor \(f(a)\) o no existe dicho valor.
La discontinuidad se llama de tipo evitable, ya que podemos evitar la discontinuidad si definiéramos:
\[ f(a) = \displaystyle \lim_{x \to a} f(x)\]
Una función presenta una discontinuidad en \(x= a\) de salto o de primera especie si existen los límites laterales y son distintos o al menos uno de ellos es infinito.
- Se dirá que la discontinuidad es de salto finito si los límites laterales son finitos.
- Se dirá que es de salto infinito si al menos uno de ellos es infinito.
Una función \(f(x)\) presenta una discontinuidad de segunda especie en el punto \(x= a\) si no existe uno de los límites laterales.
Resumiendo los tipos de dicontinuidades...
\[ \text {Discontinuidades } \left \{ \begin{array}{l}
\text {Evitable}\\
\text {De salto o primera especie}
\left \{ \begin{array}{l}
\text {Salto finito}\\
\text {Salto infinito}
\end{array} \right .
\\
\text {De segunda especie}
\end{array} \right . \]
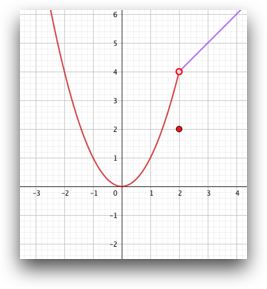
Discontinuidad evitable en \(x=2\)
|
|
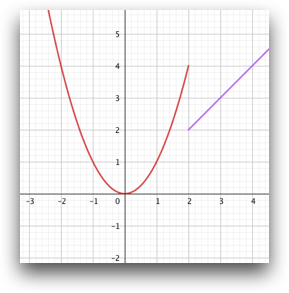
Discontinuidad de salto o primera especieDe salto finito en \(x=2\) |
|
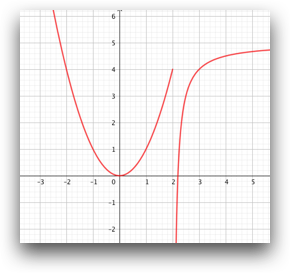
Discontinuidad de segunda especie en \(x=3\)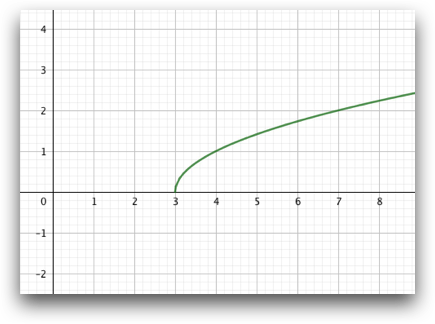 |
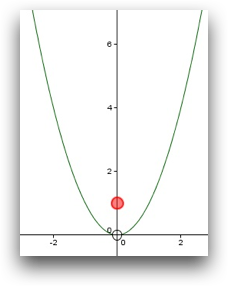
Ejercicio 3
La función \( f(x)= \left \{ \begin{array}{ccc}
x^2&si&x < 0 \\
1&si&x=0\\
x^2&si&x > 0
\end{array} \right . \) cumple que:
\[ \displaystyle \lim_{x \to 0^-} f(x)=\displaystyle \lim_{x \to 0^+} f(x) =0\]
Sin embargo \(f(0)=1\) luego la función presenta un discontinuidad evitable en \(x=0\). Se les llama evitable porque en este caso, por ejemplo, bastaría con redefinir \(f(0)=0\) para hacerla continua.
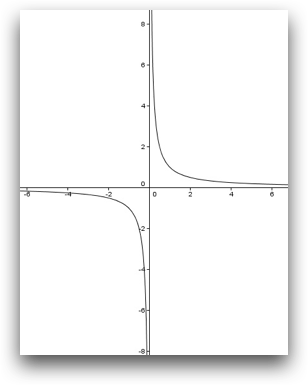
Ejercicio 4
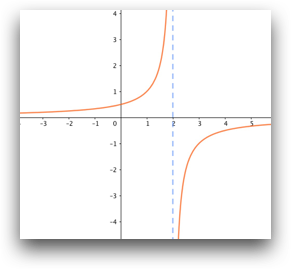
La función \( f(x) = \displaystyle \frac {1}{x} \) es un ejemplo de discontinuidad de primera especie en \( x=0 \) ya que al estudiar los límites laterales en ese punto obtenemos:
| \[ \displaystyle \lim_{x \to0^-} f(x) = -\infty \hspace{30px} \displaystyle \lim_{x \to0^+} f(x) = +\infty\] |
Ejercicio 5
Las funciones solo existen para los puntos de su dominio.
Por ejemplo, la función \( f(x) = \sqrt {x} \) tiene por dominio los números reales positivos incluido el cero. Al estudiar las discontinuidades de dicha función, podemos observar que el límite por la izquierda en \(x=0\) no existe, por lo que la función presenta una discontinuidad de segunda especie en \(x=0\).
Al calcular el límite por la derecha, observamos que \( \displaystyle \lim_{x \to 0^+} f(x)=0 \)
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Sin obra derivada 4.0