2. Distribución normal
Importante
Una variable aleatoria continua X sigue una distribución normal de media \( \mu \) y desviación típica \( \sigma \), y se representa \( X \to N(\mu , \sigma ) \) si se cumple que su función de densidad viene dada por:
| \[f(x)=\displaystyle \frac {1}{\sigma \sqrt {2 \pi} } e ^{- \frac {1}{2} \left ( \frac {x- \mu}{\sigma} \right ) ^2}\] |
La gráfica de esta función es similar a esta:

Debido a la forma que adopta se le llama campana de Gauss, y de alguna manera muestra de forma bastante visual la forma en la que suelen repartirse los datos:
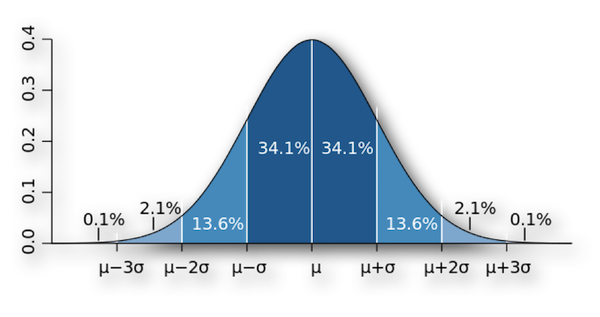
Algunos ejemplos de variables asociadas a fenómenos naturales que siguen el modelo de la normal son:
- Caracteres morfológicos de individuos (no sólo personas, sino también animales o plantas) como la estatura, el peso, perímetros, etc.
- Caracteres fisiológicos como el efecto de una dosis de un fármaco o el producido por un abono en un cultivo.
- Caracteres sociológicos como el consumo de cierto producto por un mismo grupo de individuos.
- Caracteres psicológicos como el cociente intelectual o nivel de adaptación a un medio.
- Nivel de ruido en telecomunicaciones.
- Errores cometidos al medir ciertas magnitudes.
Y en general, cualquier característica que se obtenga como suma de muchos factores independientes se ajustará a un modelo normal.
Ejercicio 02
El primer caso que vamos a estudiar es el de una normal muy concreta, la que tiene media igual a 0 y desviación típica igual a 1. La representamos por \(Z \to N(0,1)\).
En el enlace, te puedes descargar la tabla de valores de la distribución Normal N(0,1).
Lo primero que tienes que observar es que con esta tabla se calculan probabilidades del tipo \( P(Z \le a) \) donde \(Z \to N(0,1)\) y "\(a\)" el valor extremo. Es decir, se calcula el área de la zona dibujada en azul en la tabla.
Por ejemplo, vamos a calcular la probabilidad de que si \(Z\) es una variable \(N(0,1)\), un valor tomado al azar sea menor que \(1,37\).
Para calcularla, en la columna donde pone \( z_0 \) hemos de buscar la fila en la que aparece el valor entero y la primera cifra decimal, es decir, \(1,3\). Una vez encontrado, nos vamos a las columnas y buscamos en el encabezamiento la segunda cifra decimal, o sea, donde aparezca \(0,07\).
El lugar donde se cruzan esas dos búsquedas me indica la probabilidad. En nuestro caso, aparece, \(0,9147\).
Luego \(P(Z \le 1,37) = 0,9147 \)
Ejercicio 03
Calcula las siguientes probabilidades a partir de la tabla.
Usa la coma (,) para escribir los decimales.
Importante
Cálculo de probabilidades en una distribución Normal.
Si "\(a\)" es un número positivo y \(Z\) sigue una distribución \(N(0,1)\):
- \(P(Z < a)\) → A partir de la tabla de probabilidades de una distribución \(N(0,1)\)
- \(P(Z > a) = 1 - P( Z < a)\)
- \(P(Z < -a) = 1 - P( Z < a)\)
- \(P(Z > -a) = P ( Z < a )\)
- \(P(a < Z < b) = P(Z < b) - P(Z < a)\)
Ejercicio 04
Ahora te toca a ti. Calcula las siguientes probabilidades usando las propiedades vistas arriba y la tabla de probabilidades de la distribución Normal N(0,1):
\(Z\) sigue una distribución \(N(0,1)\). Calcula:
- \(P(Z ≥ 0,32)\)
- \(P(Z ≤ 0)\)
- \(P ( Z > 0,7 )\)
- \(P ( -0,51 ≤ Z ≤ 0,51)\)
- \(P (Z > - 2,63) \)
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Sin obra derivada 4.0