4.2. Distribución de la diferencia de las medias
 |
| Imagen de Anton Fomkin con licencia Creative Commons |
Veamos ahora un ejemplo que nos va a permitir comparar dos tipos de bombillas de bajo consumo de distintas marcas, pero de similares características.
Las bombillas de la marca A tienen una vida media de 11000 horas y una desviación típica de 1500 horas, mientras que las bombillas de la marca B tienen una vida media de 10000 horas y una desviación típica de 750 horas.
Supongamos que nos piden comparar las dos marcas. Cuál es la probabilidad de que una bombilla de la marca A dure mil horas más que una bombilla de la marca B.
Sean \( \overline x_A\) y \( \overline x_B\) sus respectivas medias muestrales.
Para comparar las dos marcas se considera la diferencia de sus medias, que se estima con la diferencia de las medias muestrales:
| \[ \overline x_A -\overline x_B\] |
Si se realiza este mismo proceso para otras muestras formadas por \(n_A\) bombillas de la marca \(A\) y \(n_B\) bombillas de la marca \(B\). Se irán obteniendo sus respectivas diferencias de las medias:
\[ \overline x_{A1} -\overline x_{B1}\]
\[ \overline x_{A2} -\overline x_{B2}\]
\[ \overline x_{A3} -\overline x_{B3}\]
...
Estos distintos valores dan lugar a una variable aleatoria que se representa por \( \overline X_{A} -\overline X_{B}\).
La distribución de los valores de \( \overline X_{A} -\overline X_{B}\) se llama distribución en el muestreo de la diferencia de las medias.
Importante
La distribución en el muestreo de la diferencia de las medias \( \overline X_{A} -\overline X_{B}\) tiene las siguientes características:
a. Media: La media de la distribución es la diferencia de medias: \( \mu_A -\mu _B\)
b. Desviación típica: La desviación típica es \( \sigma = \sqrt {\displaystyle \frac {\sigma_A^2}{n_A} + \displaystyle \frac {\sigma_B^2}{n_B} }\).
c. Si la población no sigue una distribución normal, pero \(n_A \ge 30\) y \( n_B \ge 30 \), la distribución \( \overline X_{A} -\overline X_{B}\) se aproxima a una normal \( N \left ( \mu_A -\mu _B ,\sqrt {\displaystyle \frac {\sigma_A^2}{n_A} + \displaystyle \frac {\sigma_B^2}{n_B} } \right )\).
Ejemplo o ejercicio resuelto
Vamos a resolver el problema con el que habíamos comenzado este apartado.
Supongamos que cogemos muestras de 50 bombillas de cada tipo. La variable estadística 
sigue una distribución N(1000 ; 237,17), pues la diferencia entre las medias de A y B es 1000 y la desviación típica aplicando la fórmula sería:
Para calcular la probabilidad de que una bombilla de la marca A dure 1000 horas más que una bombilla de la marca B sólo tendremos que calcular . Como sabemos que la variable tiene una distribución normal, vamos a calcular su valor tipificando la variable:
Es decir, una de cada dos bombillas de la clase A durará 1000 horas más que una del tipo B.
Si calculamos la probabilidad de que una de las bombillas de la marca B dure más que una de la marca A, tendremos que calcular 
Tipificando la variable tenemos:
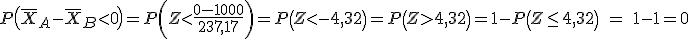
En conclusión, según el estudio que acabamos de hacer, una bombilla de la marca A durará más que una bombilla de la marca B.
AV - Reflexión
 |
| Imagen de amboo who? con licencia Creative Commons |
Una empresa ha contratado a TisBet Survey para que haga un estudio sobre la diferencia de los sueldos entre sus empleados. Están interesados en conocer si hay diferencia entre el salario medio de un hombre y de una mujer.
Para ello se han tomado una muestra aleatoria de 60 mujeres y de 40 hombres obteniendo los resultados que figuran en la tabla inferior:
| Hombres | Mujeres |
|
| Media |
1230 € |
1025 € |
| Desviación Típica |
160 € |
75 € |
Ayuda a nuestros amigos calculando la distribución en el muestreo de la diferencia de medias muestrales y la probabilidad de que la diferencia de las medias entre los salarios de los hombres y de las mujeres sea superior a 200 €.
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Sin obra derivada 4.0