5.1.Teorema de De-Moivre

No hace mucho, a las oficinas de TisBet Survey llegó la Concejalía de Urbanismo del Ayuntamiento de Sevilla para que les hiciera un estudio sobre la satisfacción de los ciudadanos con el servicio de transporte público. No sé si lo sabes, pero hace escasamente dos años (abril de 2009)

Imagen de dezpiadoz bajo licencia Creative Commons

se inauguró la primera línea de Metro, y una de las peticiones a TisBet es que analicen el nivel de uso y satisfacción que tienen los ciudadanos y ciudadanas de este nuevo medio de transporte.

La primera pregunta del estudio es clara, ¿Ha utilizado usted el Metro alguna vez? Y la respuesta es evidente, sí o no. Sólo dos posibilidades.

¿Te suena esto de dos posibilidades? Dos posibilidades..., éxito-fracaso... Exacto: Bernoulli y la binomial.

Fíjate bien. Hacemos 100 encuestas y para cada una de ellas, definimos una variable X_i (i=1, 2,... 100) a la que le damos el valor 1 si la respuesta es afirmativa y 0 en caso contrario. Además, llegamos a la conclusión de que la probabilidad de que una persona haya utilizado el Metro es de 0,31, luego la probabilidad de éxito es 0,31.

La suma de todas las puntuaciones de las variables nos da el número de respuestas afirmativas, o lo que es lo mismo, el número de éxitos obtenidos en las 100 repeticiones. Y esto si lo recuerdas, nos daba pie a una distribución binomial, en concreto, a la distribución binomial B(100; 0,31). Por tanto, si definimos una variable aleatoria S que sea la suma de los puntos de las 100 encuestas, obtenemos que:

S=ΣX_i ~ B(100; 0,31)

Todo esto de la binomial lo repasamos en el tema 3 de la unidad anterior, y como recordarás, calcular probabilidades era fácil pero un poco pesado. Imagínate que queremos calculara la probabilidad de que más de 60 personas hayan cogido el Metro. Tendríamos que calcular P(S=61), P(S=62), P(S=63),... y así hasta P(S=100). Una auténtica pesadez.

¡Vamos a utilizar el Teorema Central del Límite!

Como siempre, primero hemos de ver que se cumplen las condiciones:

• Las variables X_i i=1,... 100 son independientes, pues la muestra la hacemos de forma que la respuesta de uno no influye en la de otro.
• Las variables X_i i=1,... 100 están idénticamente distribuidas, pues todas son variables de Bernoulli con probabilidad de éxito 0,31.
• El tamaño es suficiente, pues hay 100 variables y tiene que haber más de 30.

Luego las hipótesis se cumplen.

Por otro lado, cada variable X_i hemos dicho que es una Bernoulli de parámetro 0,31. Por tanto, la media es y la desviación típica

Por tanto aplicando el Teorema Central del Límite, obtenemos que:

Y aquí sí que es fácil calcular, por ejemplo, la probabilidad de que más de 60 personas usen el Metro. Bastaría con calcular P(S > 60).

Fíjate que entonces, siempre que el número de datos sea suficiente, una Binomial se puede aproximar por una Normal, cuyos parámetros serán los que se obtienen al aplicar el Teorema Central del Límite, esto es, n·p y .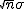

Si todavía no te lo crees, observa la siguiente escena. Ve aumentando el número de pruebas y verás que la forma de la distribución cada vez se parece más a la gráfica de una Normal.